Updated On : Jun-05,2020 Time Investment : ~30 mins

Scikit-Learn - Neural Network

Introduction

The most common type of neural network referred to as Multi-Layer Perceptron (MLP) is a function that maps input to output. MLP has a single input layer and a single output layer. In between, there can be one or more hidden layers. The input layer has the same set of neurons as that of features. Hidden layers can have more than one neuron as well. Each neuron is a linear function to which activation function is applied to solve complex problems. The output from each layer is given as input to all neurons of the next layers.

Sample Multi-Layer Perceptron

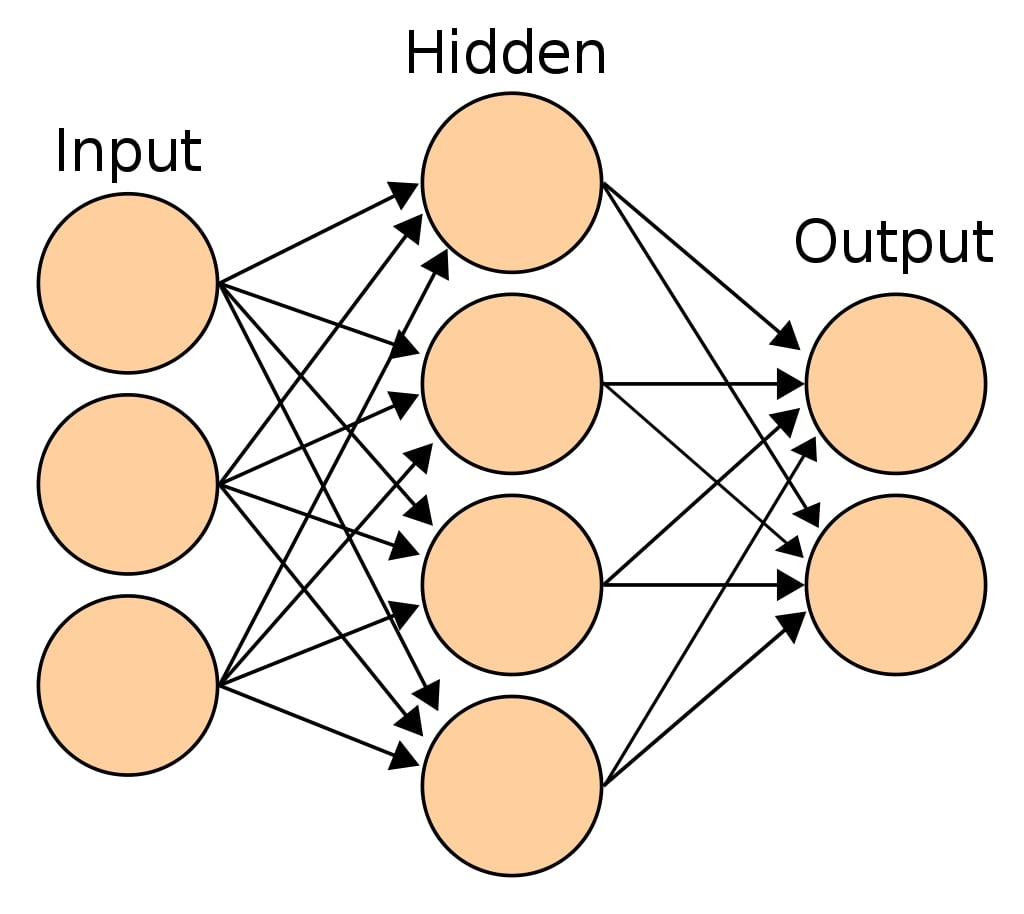
Scikit-Learn - Neural Network

sklearn provides 2 estimators for classification and regression problems respectively.

  • MLPClassifier
  • MLPRegressor

We'll start by importing necessary libraries for the tutorial.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import sklearn

import itertools
import warnings
warnings.filterwarnings('ignore')

np.set_printoptions(precision=2)
%matplotlib inline

Load Datasets

We'll be loading below mentioned two for our purpose.

  • Digits Dataset: We'll be using digits dataset which has images of size 8x8 for digits 0-9. We'll use digits data for classification tasks below.
  • Boston Housing Dataset: We'll be using the Boston housing dataset which has information about various house properties like average no of rooms, per capita crime rate in town, etc. We'll be using it for regression tasks.

Sklearn provides both of this dataset as a part of the datasets module. We can load them by calling load_digits() and load_boston() methods. It returns dictionary-like object BUNCH which can be used to retrieve features and target.

from sklearn.datasets import load_digits, load_boston

digits = load_digits()
X_digits, Y_digits = digits.data, digits.target
print('Dataset Sizes : ', X_digits.shape, Y_digits.shape)

Dataset Sizes :  (1797, 64) (1797,)

boston = load_boston()
X_boston, Y_boston = boston.data, boston.target
print('Dataset Sizes : ', X_boston.shape, Y_boston.shape)

Dataset Sizes :  (506, 13) (506,)

MLPClassifier

MLPClassifier is an estimator available as a part of the neural_network module of sklearn for performing classification tasks using a multi-layer perceptron.

Splitting Data Into Train/Test Sets

We'll split the dataset into two parts:

  • Training data which will be used for the training model.
  • Test data against which accuracy of the trained model will be checked.

train_test_split function of model_selection module of sklearn will help us split data into two sets with 80% for training and 20% for test purposes. We are also using seed(random_state=123) with train_test_split so that we always get the same split and can reproduce results in the future as well.

NOTE

Please make a note that we are also using stratify parameter which will prevent unequal distribution of all classes in train and test sets.For each classes, we'll have 80% samples in train set and 20% samples in test set. This will make sure that we don't have any dominating class in either train or test set.

from sklearn.model_selection import train_test_split

X_train, X_test, Y_train, Y_test = train_test_split(X_digits, Y_digits, train_size=0.80, test_size=0.20, stratify=Y_digits, random_state=123)
print('Train/Test Sizes : ', X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)

Train/Test Sizes :  (1437, 64) (360, 64) (1437,) (360,)

Fitting Default Model To Train Data

We'll first fit the MLPClassifier model with default parameters to our train data.

from sklearn.neural_network import MLPClassifier

mlp_classifier  = MLPClassifier(random_state=123)
mlp_classifier.fit(X_train, Y_train)

MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
              beta_2=0.999, early_stopping=False, epsilon=1e-08,
              hidden_layer_sizes=(100,), learning_rate='constant',
              learning_rate_init=0.001, max_iter=200, momentum=0.9,
              n_iter_no_change=10, nesterovs_momentum=True, power_t=0.5,
              random_state=123, shuffle=True, solver='adam', tol=0.0001,
              validation_fraction=0.1, verbose=False, warm_start=False)

Evaluating Trained Model On Test Data.

Almost all models in Scikit-Learn API provides predict() method which can be used to predict target variable on Test Set passed to it.

Y_preds = mlp_classifier.predict(X_test)

print(Y_preds[:15])
print(Y_test[:15])

print('Test Accuracy : %.3f'%mlp_classifier.score(X_test, Y_test)) ## Score method also evaluates accuracy for classification models.
print('Training Accuracy : %.3f'%mlp_classifier.score(X_train, Y_train))

[5 9 9 6 1 6 6 9 8 7 4 2 1 4 3]
[5 9 9 6 1 6 6 9 8 7 4 2 1 4 3]
Test Accuracy : 0.983
Training Accuracy : 1.000

Plotting Confusion Matrix

Below we have created a method named plot_confusion_matrix() which accepts original labels of data and predicted labels by model. It then plots a confusion matrix using matplotlib. We'll be reusing the same method for plotting the confusion matrix.

from sklearn.metrics import confusion_matrix

def plot_confusion_matrix(Y_test, Y_preds):
    conf_mat = confusion_matrix(Y_test, Y_preds)
    #print(conf_mat)
    fig = plt.figure(figsize=(6,6))
    plt.matshow(conf_mat, cmap=plt.cm.Blues, fignum=1)
    plt.yticks(range(10), range(10))
    plt.xticks(range(10), range(10))
    plt.colorbar();
    for i in range(10):
        for j in range(10):
            plt.text(i-0.2,j+0.1, str(conf_mat[j, i]), color='tab:red')

plot_confusion_matrix(Y_test, mlp_classifier.predict(X_test))

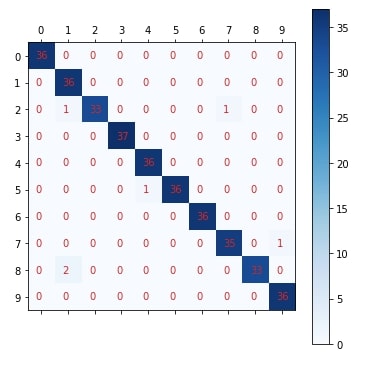
Scikit-Learn - Neural Network

Important Attributes of MLPClassifier

Below is a list of important attributes available with an MLPClassifier which can provide meaningful insights once the model is trained.

  • loss_ - It returns loss after the training process has completed.
  • coefs_ - It returns an array of length n_layers-1 where each element represents weights associated with layer i.
  • intercepts_ - It returns an array of length n_layers-1 where each element represents intercept associated with layer i's perceptrons.
  • n_iter_ - The number of iterations for which estimator ran.
  • out_activation_ - It returns name of output layer activation function.
print("Loss : ", mlp_classifier.loss_)

Loss :  0.003472868499418059

print("Number of Coefs : ", len(mlp_classifier.coefs_))

[weights.shape for weights in mlp_classifier.coefs_]

Number of Coefs :  2

[(64, 100), (100, 10)]
print("Number of Intercepts : ", len(mlp_classifier.intercepts_))

[intercept.shape for intercept in mlp_classifier.intercepts_]

Number of Intercepts :  2

[(100,), (10,)]
print("Number of Iterations for Which Estimator Ran : ", mlp_classifier.n_iter_)

Number of Iterations for Which Estimator Ran :  125

print("Name of Output Layer Activation Function : ", mlp_classifier.out_activation_)

Name of Output Layer Activation Function :  softmax

Finetuning Model By Doing Grid Search On Various Hyperparameters.

Below is a list of common hyperparameters that needs tuning for getting the best fit for our data. We'll try various hyperparameters settings to various splits of train/test data to find out best fit which will have almost the same accuracy for both train & test dataset or have quite less difference between accuracy.

  • hidden_layer_sizes - It accepts tuple of integer specifying sizes of hidden layers in multi layer perceptrons. According to size of tuple, that many perceptrons will be created per hidden layer. default=(100,)
  • activation - It specifies activation function for hidden layers. It accepts one of below strings as input. default=relu
    • 'identity' - No Activation. f(x) = x
    • 'logistic' - Logistic Sigmoid Function. f(x) = 1 / (1 + exp(-x))
    • 'tanh' - Hyperbolic tangent function. f(x) = tanh(x)
    • 'relu' - Rectified Linear Unit function. f(x) = max(0, x)
  • solver - It accepts one of below strings specifying which optimization solver to use for updating weights of neural network hidden layer perceptrons. default='adam'
    • 'lbfgs'
    • 'sgd'
    • 'adam'
  • learning_rate_init - It specifies initial learning rate to be used. Based on value of this parameter weights of perceptrons are updated.default=0.001
  • learning_rate - It specifies learning rate schedule to be used for training. It accepts one of below strings as value and only applicable when solver='sgd'.
    • 'constant' - Keeps learning rate constant through a learning process which was set in learning_rate_init.
    • 'invscaling' - It gradually decreases learning rate. effective_learning_rate = learning_rate_init / pow(t, power_t)
    • 'adaptive' - It keeps learning rate constant as long as loss is decreasing or score is improving. If consecutive epochs fails in decreasing loss according to tol parameter and early_stopping is on, then it divides current learning rate by 5.
  • batch_size - It accepts integer value specifying size of batch to use for dataset. default='auto'. The default auto batch size will set batch size to min(200, n_samples).
  • tol - It accepts float values specifying threshold for optimization. When training loss or score is not improved by at least tol for n_iter_no_change iterations, then optimization ends if learning_rate is constant else it decreases learning rate if learning_rate is adaptive. default=0.0001
  • alpha - It specifies L2 penalty coefficient to be applied to perceptrons. default=0.0001
  • momentum - It specifies momentum to be used for gradient descent and accepts float value between 0-1. It's applicable when solver is sgd.
  • early_stopping - It accepts boolean value specifying whether to stop training if training score/loss is not improving. default=False
  • validation_fraction - It accepts float value between 0-1 specifying amount of training data to keep aside if early_stopping is set.default=0.1

GridSearchCV

It's a wrapper class provided by sklearn which loops through all parameters provided as params_grid parameter with a number of cross-validation folds provided as cv parameter, evaluates model performance on all combinations and stores all results in cv_results_ attribute. It also stores model which performs best in all cross-validation folds in best_estimator_ attribute and best score in best_score_ attribute.

NOTE

n_jobs parameter is provided by many estimators. It accepts number of cores to use for parallelization. If value of -1 is given then it uses all cores. It uses joblib parallel processing library for running things in parallel in background.

We'll below try various values for the above-mentioned hyperparameters to find the best estimator for our dataset by splitting data into 5-fold cross-validation.

%%time

from sklearn.model_selection import GridSearchCV

params = {'activation': ['relu', 'tanh', 'logistic', 'identity'],
          'hidden_layer_sizes': [(100,), (50,100,), (50,75,100,)],
          'solver': ['adam', 'sgd', 'lbfgs'],
          'learning_rate' : ['constant', 'adaptive', 'invscaling']
         }

mlp_classif_grid = GridSearchCV(MLPClassifier(random_state=123), param_grid=params, n_jobs=-1, cv=5, verbose=5)
mlp_classif_grid.fit(X_train,Y_train)

print('Train Accuracy : %.3f'%mlp_classif_grid.best_estimator_.score(X_train, Y_train))
print('Test Accuracy : %.3f'%mlp_classif_grid.best_estimator_.score(X_test, Y_test))
print('Best Accuracy Through Grid Search : %.3f'%mlp_classif_grid.best_score_)
print('Best Parameters : ',mlp_classif_grid.best_params_)

Fitting 5 folds for each of 108 candidates, totalling 540 fits

[Parallel(n_jobs=-1)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=-1)]: Done  10 tasks      | elapsed:   11.4s
[Parallel(n_jobs=-1)]: Done  64 tasks      | elapsed:   57.2s
[Parallel(n_jobs=-1)]: Done 154 tasks      | elapsed:  2.8min
[Parallel(n_jobs=-1)]: Done 280 tasks      | elapsed:  5.8min
[Parallel(n_jobs=-1)]: Done 442 tasks      | elapsed:  9.1min
[Parallel(n_jobs=-1)]: Done 540 out of 540 | elapsed: 10.6min finished

Train Accuracy : 1.000
Test Accuracy : 0.986
Best Accuracy Through Grid Search : 0.980
Best Parameters :  {'activation': 'logistic', 'hidden_layer_sizes': (100,), 'learning_rate': 'constant', 'solver': 'adam'}
CPU times: user 4.09 s, sys: 2.16 s, total: 6.25 s
Wall time: 10min 40s

Plotting Confusion Matrix

plot_confusion_matrix(Y_test, mlp_classif_grid.best_estimator_.predict(X_test))

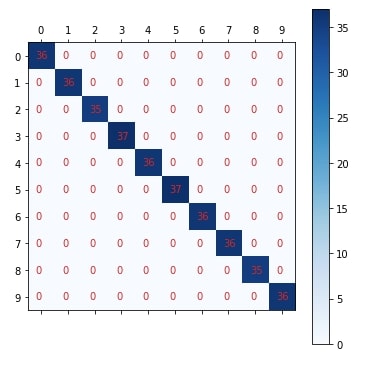
Scikit-Learn - Neural Network

MLPRegressor

MLPRegressor is an estimator available as a part of the neural_network module of sklearn for performing regression tasks using a multi-layer perceptron.

Splitting Data Into Train/Test Sets

We'll split the dataset into two parts:

  • Train data(80%) which will be used for the training model.
  • Test data(20%) against which accuracy of the trained model will be checked.
X_train, X_test, Y_train, Y_test = train_test_split(X_boston, Y_boston, train_size=0.80, test_size=0.20, random_state=123)
print('Train/Test Sizes : ', X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)

Train/Test Sizes :  (404, 13) (102, 13) (404,) (102,)

from sklearn.neural_network import MLPRegressor

mlp_regressor  = MLPRegressor(random_state=123)
mlp_regressor.fit(X_train, Y_train)

MLPRegressor(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
             beta_2=0.999, early_stopping=False, epsilon=1e-08,
             hidden_layer_sizes=(100,), learning_rate='constant',
             learning_rate_init=0.001, max_iter=200, momentum=0.9,
             n_iter_no_change=10, nesterovs_momentum=True, power_t=0.5,
             random_state=123, shuffle=True, solver='adam', tol=0.0001,
             validation_fraction=0.1, verbose=False, warm_start=False)
Y_preds = mlp_regressor.predict(X_test)

print(Y_preds[:10])
print(Y_test[:10])

print('Test R^2 Score : %.3f'%mlp_regressor.score(X_test, Y_test)) ## Score method also evaluates accuracy for classification models.
print('Training R^2 Score : %.3f'%mlp_regressor.score(X_train, Y_train))

[ 7.33 24.33 32.47 15.19 25.67 25.08 27.21  2.62 15.26 28.03]
[15.  26.6 45.4 20.8 34.9 21.9 28.7  7.2 20.  32.2]
Test R^2 Score : 0.462
Training R^2 Score : 0.510

Important Attributes of MLPRegressor

MLPRegressor has all attributes the same as that of MLPClassifier.

print("Loss : ", mlp_regressor.loss_)

Loss :  28.538174061119605

print("Number of Coefs : ", len(mlp_regressor.coefs_))

[weights.shape for weights in mlp_regressor.coefs_]

Number of Coefs :  2

[(13, 100), (100, 1)]
print("Number of Intercepts : ", len(mlp_regressor.intercepts_))

[intercept.shape for intercept in mlp_regressor.intercepts_]

Number of Intercepts :  2

[(100,), (1,)]
print("Number of Iterations for Which Estimator Ran : ", mlp_regressor.n_iter_)

Number of Iterations for Which Estimator Ran :  130

print("Name of Output Layer Activation Function : ", mlp_regressor.out_activation_)

Name of Output Layer Activation Function :  identity

Finetuning Model By Doing Grid Search On Various Hyperparameters.

MLPRegressor has almost the same parameters as that of MLPClassifier.

We'll below try various values for the above-mentioned hyperparameters to find the best estimator for our dataset by splitting data into 5-fold cross-validation.

%%time

params = {'activation': ['relu', 'tanh', 'logistic', 'identity'],
          'hidden_layer_sizes': list(itertools.permutations([50,100,150],2)) + list(itertools.permutations([50,100,150],3)) + [50,100,150],
          'solver': ['adam', 'lbfgs'],
          'learning_rate' : ['constant', 'adaptive', 'invscaling']
         }

mlp_regressor_grid = GridSearchCV(MLPRegressor(random_state=123), param_grid=params, n_jobs=-1, cv=5, verbose=5)
mlp_regressor_grid.fit(X_train,Y_train)

print('Train R^2 Score : %.3f'%mlp_regressor_grid.best_estimator_.score(X_train, Y_train))
print('Test R^2 Score : %.3f'%mlp_regressor_grid.best_estimator_.score(X_test, Y_test))
print('Best R^2 Score Through Grid Search : %.3f'%mlp_regressor_grid.best_score_)
print('Best Parameters : ',mlp_regressor_grid.best_params_)

Fitting 5 folds for each of 360 candidates, totalling 1800 fits

[Parallel(n_jobs=-1)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=-1)]: Done  10 tasks      | elapsed:    4.0s
[Parallel(n_jobs=-1)]: Done  64 tasks      | elapsed:   27.0s
[Parallel(n_jobs=-1)]: Done 154 tasks      | elapsed:  1.2min
[Parallel(n_jobs=-1)]: Done 280 tasks      | elapsed:  3.4min
[Parallel(n_jobs=-1)]: Done 442 tasks      | elapsed:  5.1min
[Parallel(n_jobs=-1)]: Done 640 tasks      | elapsed:  7.7min
[Parallel(n_jobs=-1)]: Done 874 tasks      | elapsed: 10.7min
[Parallel(n_jobs=-1)]: Done 1144 tasks      | elapsed: 13.7min
[Parallel(n_jobs=-1)]: Done 1450 tasks      | elapsed: 16.6min
[Parallel(n_jobs=-1)]: Done 1792 tasks      | elapsed: 20.1min
[Parallel(n_jobs=-1)]: Done 1800 out of 1800 | elapsed: 20.1min finished

Train R^2 Score : 0.736
Test R^2 Score : 0.597
Best R^2 Score Through Grid Search : 0.718
Best Parameters :  {'activation': 'identity', 'hidden_layer_sizes': (50, 100), 'learning_rate': 'constant', 'solver': 'lbfgs'}
CPU times: user 2.82 s, sys: 377 ms, total: 3.2 s
Wall time: 20min 6s

Please make a note during the above experiment, we have not used sgd as the value of the solver parameter because it was exploding and pushing gradients out of limit for floating-point and failure.

This ends our small tutorial explaining neural network estimators available as a part of the sklearn. Please feel free to let us know your views in the comments section.

References

Sunny Solanki  Sunny Solanki

YouTube Subscribe Comfortable Learning through Video Tutorials?

If you are more comfortable learning through video tutorials then we would recommend that you subscribe to our YouTube channel.

Need Help Stuck Somewhere? Need Help with Coding? Have Doubts About the Topic/Code?

When going through coding examples, it's quite common to have doubts and errors.

If you have doubts about some code examples or are stuck somewhere when trying our code, send us an email at coderzcolumn07@gmail.com. We'll help you or point you in the direction where you can find a solution to your problem.

You can even send us a mail if you are trying something new and need guidance regarding coding. We'll try to respond as soon as possible.

Share Views Want to Share Your Views? Have Any Suggestions?

If you want to

  • provide some suggestions on topic
  • share your views
  • include some details in tutorial
  • suggest some new topics on which we should create tutorials/blogs
Please feel free to contact us at coderzcolumn07@gmail.com. We appreciate and value your feedbacks. You can also support us with a small contribution by clicking DONATE.


Tags sklearn, neural-network
Sunny Solanki

Sunny Solanki

Software Developer | Youtuber | Bonsai Enthusiast

Subscribe to Our YouTube Channel

YouTube SubScribe

Tutorial Categories

Artificial Intelligence (83)
Data Science (84)
Digital Marketing (8)
Machine Learning (38)
Python (131)

Newsletter Subscription